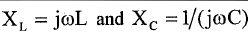Sinusoidal Steady-State Analysis (Nodal Analysis)

NODAL ANALYSIS

Given the  circuit below i(t) = 5sin(1000t) A. Find Vo(t) and io(t)

Solving this kind of problem using nodal analysis is just the same on the DC analysis.

Steps for solving the problem:

1. Analyse the problem first and simplify it (if possible).

2. Solve only for what is being asked.

3. Convert first the passive elements into a frequency domain.

where:

L is for Inductor and C is the capacitor element

4. Label the nodes and the reference node. (See figure below)

5.  Solve the circuit using your own convenient.

@ node 1

@ node 2

Simplifying it:

Matrix the given equation and solve for V1 and V2 using cramer’s rule. The result will be :

Now we have the values of V1 and V2, we can solve the Io (using the Current division):

and Vo will be

 

In this topic, nodal analysis, is very useful to solve for unknown if only there are two or more sources( voltage or current) in the given circuit. In analyzing the AC circuit, this is just the same in the DC circuit. The rules, KCL and KVL, basic formulas. The only differ is in the values used or the parameters.

 

IMPEDANCE

In the last topic about the phasor relationship of circuit elements and this is the continuation. We already know about the formulas of the three passive elements- resistor, inductor and capacitor.  (Table 1)

In the Impedance column, the Z stands for the frequency-dependent quantity (or the Impedance) and this Z is measured in Ohms (Ω).

Note: Solving for the equivalent impedance is just equal to rules in the resistance.

For example

Find  i(t) and v(t) in the circuit below:

Solution:

from the voltage source 10cos4t, we should convert it to phasor form:

Vs = 10<0º

ω = 4

The first thing to do is to convert the capacitance into a ohms value using the formula from the table 1.

Z = R + 1/jωC

Z= 5 + 1/j4 x 0.1    Ω                    note:            (j= √(-1) )

Z = 5 -2.5   Ω

to solve for current I, use ohms law

I = Vs/Z

I = 10<0º/(5-j2.5)

multiply it by the conjugate of 5-j2.5 both numerator and denominator .

I = 10(5 +j2.5) / 25 + 6.25)

I = 1.6 + j0.8

I = 1.789 < 26/57º A.

convert the I into time domain

i(t) = 1.789cos(4t + 26.57º ) A.  

The voltage across the capacitor is:

V= IZc

I/jωC  =  1.789 < 26/57º A/(j4 x 0.1)

Convert the denominator into a phasor form that is equal to 0.4<90º.

V= 4.47<-63.43º V

convert V into time domain :

v(t) = 4.47cos(4t-63.43º)  V

         

SINUSOIDS AND PHASOR

             In the late 1800’s , the battle of direct current versus alternating current began. The direct current which been develop bu Thomas Edison who has earned a lot of respect for his contribution to the field of electricity been loss by the developer of alternating current, Nikola Tesla and George Westinghouse. They established alternating current as the primary mode of electricity transmission and distribution because alternating current is more efficient and economical to transmit over a long distance compare to direct current.

So in this topic, we will focus to analyse circuits in which the source voltage or current is time-varying, or simply sinusoid current.

SINUSOID

A sinusoid is a signal that has the form of the sine and cosine fuction. The alternating current signal is usually referred to this form.

To understand better what is sinusoid, some of the example is the wave. The movements of the wave is repeating over and over again.

SINUSOID GRAPH

amplitude- the maximum value or it is Vm.

wavelength- the distance between two points.

frequency- is the number of wave cycle per second.  (Hz)

f= (no. of cycles)/time (s)

period- The time required for one complete cycle.

T= 1/f       or     T= 2π/ω

SINUSOIDAL VOLTAGE FORMULA

v(t) = Vmsinωt                                                (eq. 1)

where:

Vm is the amplitude of the sinusoid

ω is the angular frequency in radians/s

ωt the argument of the sinusoid

another general expression for the sinusoid is :

v(t) = Vmsin(ωt + φ )              (eq. 2)

where:

(ωt + φ ) is the argument and φ is the phase. These can be in radians or degrees.

IDENTITIES

A sinusoid can be expressed in either sine or cosine form using a trigonometric identities:

sin(A ± B) = sinAcosB ± cosAsinB

cos(A ± B ) = cosAcosB ± sinAsinB

With these identities, it is easy to show that

sin( ωt ± 180º) = -sinωt

cos( ωt ± 180º)= -cosωt

sin(ωt ±  90º) =  ± cosωt

cos(ωt ±  90º) =-+sinωt

EXAMPLES

1.   Find the amplitude, phase, period and frequency of the sinusoid

v(t) = 12cos(50t + 10º)

using the formula (eq. 1) we can point out the amplitude, phase and angular frequency:

Amplitude = Vm= 12V.

phase is   φ = 10º

and the angular frequency is ω = 50rad/s

The period T= 2π/ω

T=2π/(50) = 0.1257 s

frequency is f =1/T = 7.958 Hz.

2. Calculate the phase angel between v1 = -10cos(ωt + 50º)  and v2 = 12sin(ωt -10º). State which sinusoid is leading.

In order to compare v1 and v2, we must express them in the same form. If we express them in cosine form  with positive amplitudes.

v1 = -10cos(ωt + 50º)

to make it positive we must subtract 180º to the phase, the result will be:

10cos(ωt + 50º- 180º) or 10cos(ωt + 230º)                     [ 1.1]

and

v2= 12sin(ωt -10º)

to make v2 as a cosine fuction we must used the identities and the result will be:

v2= 12cos(ωt -10º-90º)

v2= 12cos(ωt -100º) or            to make it positive angle we add it to 360º

v2= 12cos(ωt +270º)                     [1.2]

Comparing the two voltages (v1 and v2) we can clearly say the v2 leads v1 by 30º. (the difference of two phasor)

PHASOR

A phasor is a complex number that represents the amplitude and phase of a sinusoid.

Phasor provide a simple means of analyzing linear circuits excited by sinusoidal sources.

Complex number z can be written in rectangular form as

z = x + jy     (1.3a)

where j = √(-1) ; x is the real part of z ; y is the imaginary part of z.

Complex number z can also be written in polar or exponential form as

z = r‹φ

where r is the magnitude of z and  φ  is the phase of z.

There are two important operations :

Multiplication

z1z2 = r1r2‹(φ1 + φ 2)

z1/z2 = (r1/r2)‹(φ1 – φ 2)

note:

Two or more polar form cannot be add or subtract. (times and divide only). And add and subtract is only applicable to rectangular form.

Time-domain  representation                                                                     Phasor- domain representation

v(t) = Vmcos(ωt + φ)                                                                                                             V = Vm‹φ

v(t) = Vmsin(ωt + φ)                                                                                                              V = Vm‹φ -90º

i(t) = Imcos(ωt + φ)                                                                                                                 I = Im‹φ

i(t) = Vmsin(ωt + φ)                                                                                                               I = Im‹φ

DERIVATIVES

dv/dt      =   jωV                                                 ∫vdt        = V/jω

di/dt      =   jωI                                                  ∫idt        = I/jω

Examples

1. Evaluate this complex number:

a.  (40‹ 50º + 20<(-30º ))     

first is to convert polar to rectangular using calculator

Rec ( 40,50)  = 25.71 +j30.64         (this is using the standard form z=x +jy)

Rec(20,-30) = 17.32 -j10

adding them gives:

43.03 + j20.64 or 47.72<25.63º  using the calculator Pol function.

2. Transform sinusoids to phasor

i = 6cos(50t _ 40º) A

just copy the angle and Vm which leads to

I= 6<(-40º) A

PHASOR RELATIONSHIPS FOR CIRCUIT ELEMENTS

We will begin to the resistor:

v =iR (ohm’s law)

v= RImcos(ωt + φ)

the phasor form of this voltage is V = RIm<φ

Inductor:

v = Ldi/dt

v= -ωLImsin(ωt + φ) or v = ωLImcos(ωt + φ+90)

which will be transform to the phasor

V= ωLIm<( φ+90)

Capacitor

i = Cdv/dt

I= jωCV

V= I/(jωC)